
Vektörler Konu Anlatımı ve İçeriği
Vektörler, büyüklük ve yön bilgisi taşıyan matematiksel nesnelerdir. Matematik ve fizik başta olmak üzere çeşitli alanlarda büyük öneme sahiptirler. Vektörlerin tanımı, bileşenleri, özellikleri ve uygulama alanları, bu çalışmada detaylı bir şekilde incelenmiştir.
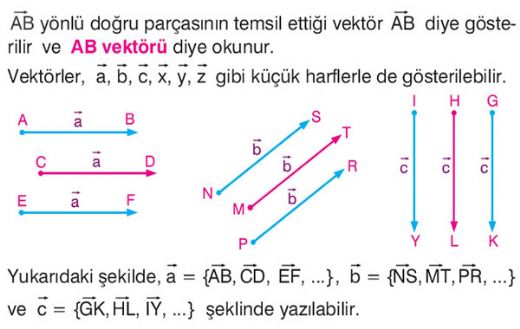
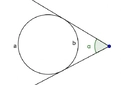
Vektörler Konu Anlatımı Vektörler, matematik ve fizik gibi birçok alanda önemli bir yere sahip olan, büyüklük ve yön bilgisi taşıyan matematiksel nesnelerdir. Bu makalede, vektörlerin tanımı, bileşenleri, özellikleri ve uygulama alanları detaylı bir şekilde ele alınacaktır. Vektörlerin Tanımı Vektör, bir başlangıç noktası ve bir bitiş noktası olan, yön ve büyüklük belirten bir ok ile temsil edilebilir. Vektörler genellikle "A" ve "B" noktaları arasında bir ok ile gösterilir ve şu şekilde tanımlanır:
Bu durumda, vektör A'dan B'ye, vektörün bileşenleri (x2 - x1, y2 - y1) şeklinde ifade edilebilir. Vektörlerin Bileşenleri Vektörler, bileşenleri aracılığıyla daha kolay analiz edilebilir. Bir vektör genellikle iki veya üç boyutlu uzayda temsil edilir. İki boyutlu bir vektör (x, y) olarak ifade edilirken, üç boyutlu bir vektör (x, y, z) şeklinde yazılır. Her bir bileşen, ilgili eksende vektörün büyüklüğünü gösterir. Vektörlerin Özellikleri Vektörlerin bazı önemli özellikleri şunlardır:
Vektörlerin Uygulama Alanları Vektörler, birçok farklı alanda kullanılmaktadır. Bu alanlardan bazıları şunlardır:
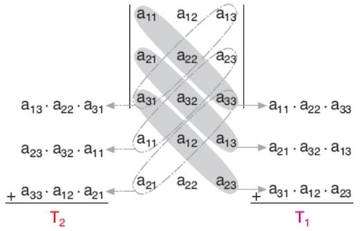
Sonuç Vektörler, matematiksel ve fiziksel hesaplamalarda temel bir yapı taşıdır. Büyüklük ve yön bilgisi taşıyan bu nesneler, çeşitli alanlarda uygulama bulmakta ve karmaşık sistemlerin analizine olanak tanımaktadır. Vektörlerin özellikleri ve bileşenleri, birçok bilim dalında kullanılabilirliklerini artırmaktadır. Ekstra Bilgiler Vektörlerin kullanımı, daha karmaşık matematiksel yapılar olan matrisler ve tensörlerle de ilişkilidir. Özellikle çok boyutlu analizlerde bu yapıların bir arada kullanımı yaygındır. Vektörlerin geometrik yorumları, daha iyi anlaşılmalarını sağlar ve birçok görselleştirme tekniği bu yorumlara dayanmaktadır. Vektör alanları gibi kavramlar, diferansiyel denklemlerin çözümünde ve fiziksel sistemlerin modellenmesinde önemli bir yere sahiptir. |
































Vektörler hakkında verdiğiniz bilgiler oldukça kapsamlı. Özellikle vektörlerin yön ve büyüklük açısından bir arada değerlendirilmesinin ne kadar önemli olduğunu vurgulamanız dikkat çekici. Vektörel ve skaler büyüklükler arasındaki farkları net bir şekilde açıklamanız, konunun anlaşılmasını kolaylaştırıyor. Sizce, günlük hayatta vektörlerin kullanımına örnekler vererek bu bilgileri daha da somut hale getirmek mümkün mü? Örneğin, bir sporda ya da bir ulaşım aracında vektörlerin nasıl devreye girdiği hakkında daha fazla bilgi paylaşabilir misiniz?
Baybek,
Vektörlerin Günlük Hayattaki Kullanımı konusundaki düşüncelerinizi paylaştığınız için teşekkür ederim. Evet, vektörlerin günlük hayatta nasıl kullanıldığına dair örnekler vermek, konunun daha anlaşılır hale gelmesine yardımcı olabilir.
Spor Örnekleri: Örneğin, bir futbol oyununda topun hareketi vektörlerle tanımlanabilir. Topun hangi yöne gittiği ve ne kadar hızlı gittiği, bir vektörle temsil edilir. Bir oyuncunun topa vurma açısı ve kuvveti de vektör olarak değerlendirilir. Bu sayede, oyuncuların stratejilerini belirlemesi ve rakiplerini analiz etmesi daha kolay hale gelir.
Ulaşım Araçları: Bir otomobilin hareketi de vektörlerle ifade edilir. Otomobilin hızı, yönüyle birlikte göz önünde bulundurulmalıdır. Örneğin, bir otomobil saatte 60 km hızla kuzeye doğru gidiyorsa, bu bilgi hem büyüklük (hız) hem de yön (kuzey) içeren bir vektörle tanımlanır. Ayrıca, navigasyon sistemleri, yönlendirme yaparken bu vektörleri kullanarak en kısa veya en hızlı yolları belirler.
Bu tür somut örnekler, vektörlerin önemini ve günlük hayattaki pratik uygulamalarını daha iyi anlamamıza yardımcı oluyor. Başka konularda da tartışmak isterseniz, her zaman buradayım!