Üslü ifadeler, matematikte sıkça kullanılan ve genellikle sayıları ve değişkenleri belirli bir kuvvetle çarpan ifadelerdir. Bu yazıda, üslü ifadelerin tanımı, özellikleri, işlemleri ve uygulamaları detaylı bir şekilde ele alınacaktır. 1. Üslü İfadelerin TanımıÜslü ifade, bir sayının veya değişkenin kendisiyle belirli bir sayıda çarpılması sonucunda elde edilen ifadelerdir. Matematiksel olarak, a sayısının n kuvveti şöyle ifade edilir: a^n = a × a × a ×... × a (n kez) Burada a taban, n ise üslü sayı ya da kuvvettir. Üslü ifadeler, genellikle daha kısa ve öz bir şekilde büyük sayıları ifade etmek için kullanılır. 2. Üslü İfadelerin ÖzellikleriÜslü ifadelerin bazı temel özellikleri şunlardır:
Bu özellikler, üslü ifadelerin çeşitli matematiksel işlemlerle bir araya getirilmesini ve sadeleştirilmesini kolaylaştırmaktadır. 3. Üslü İfadelerin İşlemleriÜslü ifadelerle yapılan işlemler, temel matematik işlemlerinin üslü sayılarla birleştirilmesiyle gerçekleştirilir. Aşağıda, üslü ifadelerle ilgili bazı örnek işlemler yer almaktadır:
Bu işlemler, üslü ifadelerin daha karmaşık matematiksel ifadelerde nasıl kullanılabileceğine dair iyi örnekler sunmaktadır. 4. Üslü İfadelerin UygulamalarıÜslü ifadelerin çeşitli alanlarda önemli uygulamaları bulunmaktadır. Bunlar arasında:
Bu uygulamalar, üslü ifadelerin matematiksel temellerinin ötesinde, bilim ve mühendislik gibi alanlarda ne denli önemli olduğunu göstermektedir. 5. Ekstra BilgilerÜslü ifadelerle ilgili bazı önemli noktalar şunlardır:
Bu ekstra bilgiler, üslü ifadelerin daha derinlemesine anlaşılmasına katkı sağlamaktadır. Sonuç olarak, üslü ifadeler matematikte önemli bir yere sahiptir ve çeşitli alanlarda geniş bir uygulama yelpazesi sunmaktadır. Bu makalede, üslü ifadelerin tanımından özelliklerine, işlemlerinden uygulamalarına kadar birçok önemli konu ele alınmıştır. Matematiksel düşünme becerilerini geliştirmek ve bu ifadeleri daha iyi anlamak için pratik yapmak ve çeşitli problemler üzerinde çalışmak oldukça faydalıdır. |
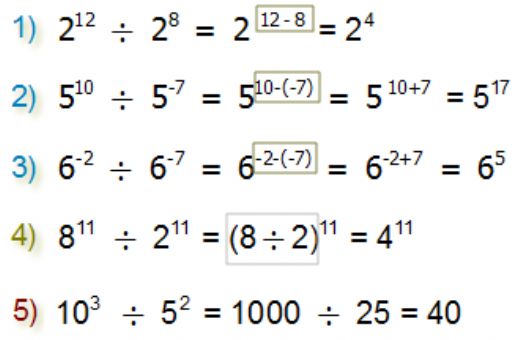
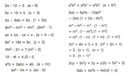
Matematik sınavında üslü sayıların eksi üstlerini hesaplarken neden hep hata yapıyorum? Özellikle negatif sayıların üstlerini alırken karışıklık yaşıyorum, bu konuda basit bir yöntemle nasıl daha iyi olabiliriz?
Cevap yazYıldırım Bey,
Üslü sayılar konusunda karışıklık yaşaman oldukça anlaşılır bir durum. Üslü sayılar negatif olduğunda hata yapmamak için şu adımları izleyebilirsin:
1. Parantez Kullanımı: Negatif sayıların üslü işlemlerinde parantez kullanmak çok önemlidir. Örneğin, \((-2)^3\) ile \(-2^3\) arasında fark vardır. Birincisi -2'nin küpüdür ve sonuç -8'dir. İkincisi ise 2'nin küpü olup negatif işaret sonradan eklenir ve sonuç -8'dir.
2. Kural Bilgisi: Negatif bir sayının çift kuvveti pozitif, tek kuvveti ise negatif olacaktır. Örneğin, \((-2)^2 = 4\) ve \((-2)^3 = -8\).
3. Pratik Yapmak: Konu üzerinde bol bol pratik yaparak kafa karışıklığını aşabilirsin. Çeşitli örnekler çözmek ve bu örnekler üzerine düşünmek konuyu kavramanı kolaylaştıracaktır.
4. Temel Kuralları Hatırlamak: Üslü sayıların temel kurallarını hatırlamak ve bunları sık sık gözden geçirmek de faydalı olacaktır. Bu kuralları küçük notlar halinde defterine yazabilirsin.
Bu adımları takip ederek üslü sayılar konusundaki hatalarını azaltabilir ve daha iyi bir performans gösterebilirsin. Başarılar dilerim!