Permütasyon Konu Anlatımı Permütasyon, bir kümenin elemanlarının farklı dizilişlerini hesaplama yöntemidir. Bu konu, genellikle 10. sınıf matematik müfredatında ayrıntılı bir şekilde ele alınmaktadır. Permütasyon sorularını çözebilmek için ayrıca faktöriyel konusuna da hakim olmanız gerekmektedir. Şimdi, permütasyon konusunu detaylı bir şekilde anlatmaya çalışacağız. Permütasyon Nedir? Permütasyon, aslında sıralama yapmak için kaç farklı yöntem kullanabileceğimizin cevabını aramaktadır. Örneğin, n elemanlı bir kümenin sıralanışı P(n, n) şeklinde yazılır ve n! ile sonuç bulunur. Ayrıca, n elemanlı bir kümenin r elemanlı alt kümelerinin sayısını bulmak için ise P(n, r) = n! / (n-r)! formülü kullanılır. Permütasyon konu anlatımında önemli bir püf noktası, permütasyonda seçim yapılmaz; seçimi yapılmış elemanların sıralanışı söz konusudur. Ayrıca, permütasyon birebir ve örten fonksiyon olmalıdır. Düz Permütasyon Düz permütasyon, n kadar elemanın yatay bir doğru üzerinde sıralanışını hesaplamadır. Düz permütasyon sorularının çözümü oldukça kolaydır. Herhangi bir seçim yapmadan sıralamasını yapmanız gerekmektedir. Örnek: 4 aşçı ve 2 kalfa kaç farklı şekilde sıralanır? (4 + 2)! = 6! = 1 × 2 × 3 × 4 × 5 × 6 = 720 olur. Dairesel Permütasyon Dairesel permütasyon, n kadar elemanın bir daire üzerindeki sıralanışını hesaplama yöntemidir. Burada, n elemanlı permütasyon için (n-1)! formülü kullanılır. Tekrarlı Permütasyon Tekrarlı permütasyon, n kadar elemanın x kadar birbirinin aynısı ve y kadar birbirinin aynısı olma durumunda hesaplanır. Bu durumda, n! / (x! × y! × z!) formülü kullanılır. Permütasyonun Uygulama Alanları Permütasyon, sadece matematikte değil, aynı zamanda birçok farklı alanda da uygulama alanı bulur:
Sonuç Permütasyon, elemanların farklı sıralanışlarını hesaplamak için kullanılan temel matematiksel yöntemlerden biridir. Düz, dairesel ve tekrarlı permütasyon gibi farklı türleri bulunmaktadır ve bu türler, çeşitli formüllerle hesaplanır. Permütasyon, sadece matematik derslerinde değil, aynı zamanda çeşitli bilim dallarında da geniş bir uygulama alanı bulmaktadır. |
Necdet
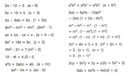
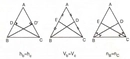
24 Temmuz 2024 ÇarşambaPermütasyonun düz ve dairesel türleri arasındaki fark tam olarak nedir? Dairesel permütasyon neden (n-1)! formülü ile hesaplanıyor?
Cevap yazAdmin
24 Temmuz 2024 ÇarşambaMerhaba Necdet,
Permütasyonun düz ve dairesel türleri arasındaki temel fark, elemanların yerleştirilme biçiminden kaynaklanır. Düz permütasyonda elemanlar belirli bir sırayla dizilir ve her bir elemanın yeri önemlidir. Örneğin, A, B, C elemanlarının düz permütasyonu ABC, ACB, BAC, BCA, CAB, CBA gibi sıralamalardan oluşur ve toplamda n! (n faktöriyel) kadar farklı sıralama vardır.
Dairesel permütasyonda ise elemanlar bir çember üzerinde yerleştirilir ve çemberin herhangi bir noktasından başlamak aynı permütasyon olarak kabul edilir. Bu nedenle, aynı elemanlar farklı başlangıç noktalarından sayıldığında farklı permütasyonlar oluşturmaz. Bu durumu hesaba katmak için, çemberdeki n elemanı (n-1)! şeklinde hesaplarız. Çünkü bir elemanın sabit bir noktada olduğunu varsayarak diğer (n-1) elemanın sıralanmasını düşünürüz. Örneğin, 4 elemanın dairesel permütasyonu (4-1)! = 3! = 6 farklı sıralama şeklinde hesaplanır.
Umarım bu açıklama yardımcı olur. Başka soruların olursa lütfen sormaktan çekinme.
Selamlar,