
Limit Konu Anlatımı ve İçeriği
Limit kavramı, matematikte bir fonksiyonun belirli bir noktaya yaklaşırken aldığı değerleri tanımlamak için kullanılır. Analiz ve kalkülüs gibi alanlarda önemli bir yere sahip olan limit, farklı hesaplama yöntemleri ve uygulamaları ile matematiksel düşünmeyi geliştirmeye yardımcı olur.
Limit Konu Anlatımı ve İçeriği Limit, matematikte bir fonksiyonun belirli bir noktaya yaklaşırken aldığı değeri belirlemek için kullanılan temel bir kavramdır. Limit kavramı, özellikle analiz ve kalkülüs alanlarında büyük öneme sahiptir. Bu makalede limitin tanımı, hesaplama yöntemleri ve uygulamaları üzerinde durulacaktır. Limitin Tanımı Limit, bir fonksiyonun bir noktaya yaklaşması durumunda ne değeri aldığına dair bir kavramdır. Matematiksel olarak, bir f(x) fonksiyonu x değeri a'ya yaklaştıkça L değerine yaklaşırsa, bu durum şu şekilde ifade edilir:
Burada, "lim" limiti belirtir, "x → a" x'in a'ya yaklaşmasını ifade eder ve "L" limit değerini temsil eder. Limitin varlığı, fonksiyonun belirli bir noktada sürekliliği ile doğrudan ilişkilidir. Limit Hesaplama Yöntemleri Limit hesaplama sürecinde farklı yöntemler kullanılabilir. Bu yöntemler arasında en yaygın olanları şunlardır:
Doğrudan Yerine Koyma Yöntemi Bu yöntemde, limit alınacak noktada fonksiyonun değeri doğrudan yerine konularak hesaplanır. Eğer bu işlem sonucunda belirli bir sayı elde ediliyorsa, limit değeri budur. Ancak, eğer işlem sonucunda 0/0 gibi belirsizlik durumları ortaya çıkıyorsa, diğer yöntemlere başvurulması gerekmektedir. Çarpanlara Ayırma Yöntemi Bu yöntemde, limit alınacak fonksiyonun ifadesi çarpanlarına ayrılarak, belirsizlik durumlarından kurtulmaya çalışılır. Eğer çarpanlar arasında ortak bir terim varsa, bu terim sadeleştirilerek limit hesaplanabilir. Rasyonelizasyon Yöntemi Rasyonelizasyon, özellikle köklü ifadelerin limitini hesaplamak için kullanılır. Bu yöntemde, köklü ifadelerin çarpanı ile hem payı hem de paydayı çarparak belirsizlikten kurtulma amaçlanır. L'Hôpital Kuralı Bu kural, 0/0 veya ∞/∞ belirsizlik durumlarında kullanılabilir. L'Hôpital kuralı, limitin hesaplanması için türev alma işlemini kullanır. Eğer lim (x → a) f(x) / g(x) belirsiz bir durumdaysa, şu formül uygulanır:
Burada f'(x) ve g'(x) sırasıyla f(x) ve g(x) fonksiyonlarının türevleridir. Limitin Uygulamaları Limit kavramı, matematiksel analizde birçok uygulama alanına sahiptir. Bu alanlar arasında:
Limit, matematiksel düşüncenin temel taşlarından biridir. Fonksiyonların davranışını anlamak için kritik bir öneme sahiptir. Limit kavramı ile birlikte, birçok matematiksel ve fiziksel problem çözülebilir hale gelir. Bu nedenle, limitin doğru bir şekilde anlaşılması ve uygulanması, matematik eğitiminin önemli bir parçasıdır. Sonuç olarak, limit kavramı matematiksel analizde çok önemli bir yere sahiptir. Limitin tanımı, hesaplama yöntemleri ve uygulamaları hakkında bilgi sahibi olmak, hem teorik hem de pratik anlamda matematiksel düşünme becerilerini geliştirecektir. Limit, yalnızca bir matematiksel kavram olmanın ötesinde, birçok alanın temelini oluşturmaktadır. Bu bağlamda, limitin incelenmesi ve anlaşılması, matematiğin evrensel dilini anlamak için elzemdir. |










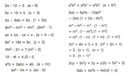























Limit kavramını gündelik yaşamda anlattığınız bu yolla anlamaya çalıştım ama kafam biraz karıştı. Gerçekten her adımda yarısına yaklaşarak 10 metreyi tamamlayamıyor muyuz? Bu durumda matematiksel olarak nasıl bir sonuç elde ediyoruz?
Nisa,
Limit Kavramı matematikte oldukça önemli bir yer tutar ve günlük yaşamda da sıkça karşılaştığımız bir konsepttir. Sorunuzu yanıtlamak için, örneğin bir koşucunun 10 metreyi tamamlaması üzerine düşünelim. Eğer koşucu her adımında, hedefe olan mesafenin yarısını kat ediyorsa, ilk adımda 5 metre, ikinci adımda 2.5 metre, üçüncü adımda 1.25 metre, şeklinde devam eder. Bu durumda, her adımda mesafe azalırken, koşucu asla tam 10 metreyi tamamlayamaz gibi görünüyor. Ancak matematiksel olarak bunun doğru olmadığını söyleyebiliriz.
Matematiksel Sonuç olarak, bu durumu bir "sonsuz serinin" toplamı olarak düşünebiliriz. Her adımın mesafesinin toplamı, 5 + 2.5 + 1.25 + ... şeklinde bir dizi oluşturur. Bu dizinin toplamı, limit kavramı sayesinde 10 metreye yaklaşır. Matematikte bu tür durumlar, limitler aracılığıyla ifade edilir ve bu örnekte limit, koşucunun 10 metreyi tamamladığını gösterir.
Sonuç olarak, her adımda mesafe yarıya inmesine rağmen, aslında limitte 10 metreyi tamamladığı sonucuna ulaşırız. Yani matematiksel olarak, koşucu 10 metreyi tamamlayabilir, fakat her adımda mesafeyi yarıya indirdiği için, fiziksel olarak adım atmaya devam ederken bu süreci sonsuz bir dizi gibi düşünebiliriz. Bu, limitin ne kadar güçlü bir kavram olduğunu gösteriyor. Anlayışınıza katkıda bulunmasını umarım!