
Oran Orantı Konu Anlatımı ve İçeriği
Oran ve orantı, matematikte iki sayının karşılaştırılması ve bu oranlar arasındaki eşitlikleri ifade eder. Gündelik hayatta yaygın kullanım alanlarına sahip olan bu kavramlar, pratik problemlerin çözümünde önemli bir rol oynamaktadır. Bu makalede, oran ve orantının temel tanımları ve hesaplama yöntemleri ele alınmaktadır.
Oran Orantı Konu AnlatımıOran ve orantı matematiksel kavramlardır ve birçok farklı alanda, özellikle de günlük hayatta sıkça kullanılmaktadır. Oran, iki sayının birbirine olan karşılaştırması iken, orantı bu oranların eşitliği anlamına gelir. Bu makalede, oran ve orantının ne olduğu, nasıl hesaplandığı ve uygulama alanları ele alınacaktır. Oran Nedir? Oran, iki niceliğin birbirine bölünmesiyle elde edilen değerdir. Genellikle "a: b" şeklinde gösterilir. Bu gösterim, a sayısının b sayısına oranını ifade eder. Oranlar genellikle iki ya da daha fazla nicelik arasında ilişki kurmak için kullanılır. Örnek Oran HesaplamaBir sınıfta 20 erkek ve 15 kız öğrenci olduğunu varsayalım. Bu durumda erkeklerin kızlara oranı şu şekilde hesaplanır:
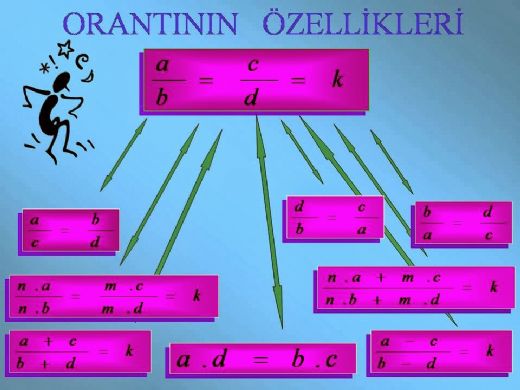
Yani, sınıftaki erkeklerin kızlara oranı 4: 3'tür. Orantı Nedir? Orantı, iki oran arasında bir eşitlik durumunu ifade eder. Yani, a: b = c: d şeklinde yazılır. Burada, a ve b ilk oranın terimleri, c ve d ise ikinci oranın terimleridir. Orantı, iki oran arasında bir ilişki kurar ve bu nedenle matematiksel problemlerde sıklıkla kullanılır. Orantı Örnekleri Bir orantının doğru olup olmadığını kontrol etmek için çapraz çarpma yöntemi kullanılabilir. Örneğin:
Görüldüğü gibi, her iki çapraz çarpma işlemi de 12'ye eşit olduğu için bu orantı doğrudur. Oran ve Orantının Uygulama Alanları Oran ve orantı kavramları, birçok alanda önemli bir rol oynamaktadır. Örneğin:
Sonuç Oran ve orantı, matematiğin temel kavramları arasında yer almakta ve birçok pratik uygulama alanına sahiptir. Bu kavramların anlaşılması, matematiksel becerileri geliştirmek ve günlük yaşamda karşılaşılan problemleri çözmek için son derece önemlidir. Oran ve orantının doğru bir şekilde kullanılması, analitik düşünme yeteneğini de güçlendirmektedir. Ekstra Bilgiler Oran ve orantı ile ilgili bazı ilginç bilgiler şunlardır:
Bu bilgiler, oran ve orantının sadece matematiksel bir kavram olmadığını, aynı zamanda günlük yaşamda ve farklı disiplinlerde nasıl bir rol oynadığını göstermektedir. |
































Oran ve orantının tanımları ve özelliklerini anlamakta zorlanıyorum, daha basit bir açıklama yapabilir misiniz? Orantı problemlerini çözerken hangi adımları izlemeliyim?
Tabii Uyarel, oran ve orantıyı basit bir şekilde açıklayayım.
Oran: İki sayının birbirine bölümüdür. Örneğin, 4 ve 2 sayılarının oranı 4/2 = 2'dir.
Orantı: İki oranın birbirine eşit olduğu duruma denir. Örneğin, 4/2 ile 8/4 oranları eşittir, bu nedenle bu bir orantıdır.
Orantı problemlerini çözerken şu adımları izleyebilirsin:
1. Problemi dikkatlice oku ve verilen oranları belirle.
2. Orantının eşit olduğu durumu kur.
3. Bilinmeyeni bulmak için denklem oluştur ve çöz.
4. Çözümünü kontrol et ve doğru olduğundan emin ol.
Umarım bu açıklama işine yarar, Uyarel!