
9 Sınıf Kümeler Konu Anlatımı ve İçeriği
Bu içerik, 9. sınıf matematik müfredatında yer alan kümeler konusunu kapsamlı bir şekilde ele almaktadır. Kümelerin tanımı, gösterim biçimleri, türleri ve temel işlemleri hakkında bilgi vererek, öğrencilerin matematiksel düşünme becerilerini geliştirmeyi amaçlamaktadır.
9 Sınıf Kümeler Konu Anlatımı ve İçeriğiKüme, matematikte nesnelerin bir araya getirilmesiyle oluşan bir topluluktur. 9. sınıf matematik müfredatında kümeler konusu, temel matematiksel kavramların anlaşılması açısından büyük bir öneme sahiptir. Bu makalede, kümelerle ilgili temel kavramlar, kümelerin gösterim biçimleri ve çeşitli alt kümeleri detaylı bir şekilde ele alınacaktır. Küme Nedir? Küme, belirli bir özelliği paylaşan nesnelerin bir araya getirildiği bir topluluktur. Nesneler, kümenin elemanları olarak adlandırılır. Örneğin, {1, 2, 3} kümesi, 1, 2 ve 3 sayılarının elemanlarıdır. Kümelerin Gösterimi Küme gösteriminde iki temel yöntem bulunmaktadır:
Küme Türleri Küme türleri, matematiksel işlemler ve uygulamalar açısından önem taşır. Aşağıda, temel küme türleri listelenmiştir:
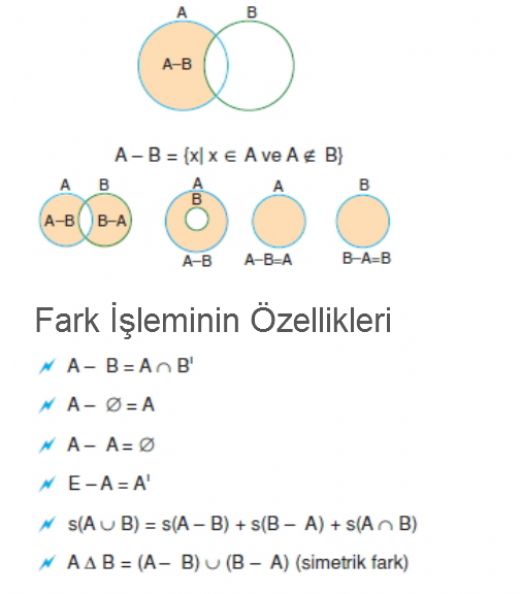
Küme İşlemleri Küme işlemleri, kümeler arasındaki ilişkileri anlamak ve analiz etmek için kullanılır. Temel küme işlemleri şunlardır:
Sonuç 9. sınıf matematik müfredatında kümeler konusu, temel matematiksel kavramların anlaşılmasında önemli bir yerdir. Kümeler, matematiksel düşünmenin temeli olup, pek çok alanda uygulama alanı bulmaktadır. Bu makalede, kümelerin tanımı, gösterimi, türleri ve işlemleri detaylı bir şekilde ele alınmıştır. Öğrencilerin bu konudaki bilgileri, matematiksel düşünme becerilerini geliştirecek ve daha karmaşık kavramları anlamalarına yardımcı olacaktır. Ekstra Bilgiler Küme teorisi, matematiğin birçok dalında, özellikle de mantık, istatistik ve bilgisayar bilimlerinde önemli bir rol oynamaktadır. Kümeler, veri analizi ve algoritma tasarımı gibi konularda da sıklıkla yer almaktadır. Öğrencilerin bu konudaki bilgilerini derinleştirmeleri, ileri düzey matematiksel kavramları anlamalarına yardımcı olacaktır. |
































Kümelerin tanımını anlamakta zorlanıyorum. Sınıfımızın başarılı öğrencileri neden iyi tanımlanmış bir küme değil? Bu konuda daha fazla örnek verebilir misiniz? Ayrıca, Venn şeması ile ilgili daha fazla örnek çalışması yapabileceğim kaynaklar önerebilir misiniz?
Merhaba Abdi,
Kümelerin tanımını anlamakta zorlanman gayet normal, özellikle ilk kez karşılaşıldığında biraz kafa karıştırıcı olabilir. Kümelerin kesin ve belirli özelliklere dayalı olarak tanımlanması gerekir. "Sınıfımızın başarılı öğrencileri" gibi bir tanım belirsizdir, çünkü "başarılı" kavramı herkese göre değişebilir. Kimine göre başarı, sadece akademik notlarla ilgiliyken, başkasına göre sosyal yetenekler ve diğer faaliyetlerdeki başarıları da içerebilir. Bu belirsizlik, bu tür bir grubun kesin bir küme olarak tanımlanmasını zorlaştırır.
Örnek:
- Üçten fazla kenarı olan geometri şekilleri bir küme olabilir: {üçgen, kare, beşgen, altıgen...}
- 10'dan küçük pozitif tam sayılar bir küme olabilir: {1, 2, 3, 4, 5, 6, 7, 8, 9}
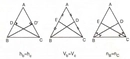
Venn Şemaları:
Venn şemaları ile ilgili daha fazla örnek ve çalışma yapabileceğin kaynaklar olarak aşağıdaki kitapları ve web sitelerini önerebilirim:
- "Discrete Mathematics and Its Applications" by Kenneth H. Rosen
- "Schaum's Outline of Set Theory and Related Topics" by Seymour Lipschutz
- Khan Academy'nin Set Theory ve Venn Diagrams ile ilgili videoları
- Math is Fun web sitesi, özellikle Venn Şemaları bölümü
Umarım bu bilgiler işine yarar, Abdi. Herhangi bir sorunda yardım etmeye hazırım. Başarılar dilerim!