Karmaşık Sayılar Konu Anlatımı

Karmaşık sayılar, matematikte geniş bir uygulama alanına sahip olan ve reel sayıların ötesine geçen bir sayı sistemidir. Bu sistem, matematiksel analiz, mühendislik, fizik ve birçok bilim dalında önemli bir yere sahiptir. Karmaşık sayılar, reel ve sanal kısımlardan oluşur ve genellikle "a + bi" biçiminde ifade edilir. Burada "a" reel kısmı, "b" ise sanal kısmı temsil ederken, "i" sanal birimdir ve "i² = -1" eşitliğini sağlar. Bu makalede, karmaşık sayıların tanımı, bileşenleri, temel işlemleri ve uygulamaları üzerinde durulacaktır.

Karmaşık bir sayı, iki bileşenden oluşur:

• Reel Kısım: "a" değeri, karmaşık sayının reel kısmını temsil eder.
• Sanal Kısım: "b" değeri, karmaşık sayının sanal kısmını temsil eder.

Karmaşık sayılar genellikle "z = a + bi" şeklinde gösterilir. Burada "z", karmaşık sayıyı ifade ederken, "a" ve "b" reel sayılardır.

Karmaşık sayıların bazı temel özellikleri şunlardır:

• Karmaşık sayıların toplama ve çıkarma işlemleri, reel sayıların işlemleri gibi gerçekleştirilir.
• Çarpma ve bölme işlemlerinde karmaşık sayılar, özel kurallara tabi tutulur.
• Karmaşık sayılar, karmaşık düzlemde gösterilebilir, burada yatay eksen reel kısmı, dikey eksen ise sanal kısmı temsil eder.

Karmaşık sayıların toplama ve çıkarma işlemleri, bileşenlerine göre gerçekleştirilir. İki karmaşık sayı "z₁ = a + bi" ve "z₂ = c + di" olsun. Bu durumda:

• Toplama: z₁ + z₂ = (a + c) + (b + d) i
• Çıkarma: z₁ - z₂ = (a - c) + (b - d) i

Karmaşık sayıların çarpma ve bölme işlemleri, aşağıdaki gibi gerçekleştirilir:

• Çarpma: z₁ z₂ = (a + bi) (c + di) = ac + adi + bci + bd(i²) = (ac - bd) + (ad + bc) i
• Bölme: z₁ / z₂ = (a + bi) / (c + di) = [(a + bi) (c - di)] / (c² + d²) = [(ac + bd) + (bc - ad) i] / (c² + d²)

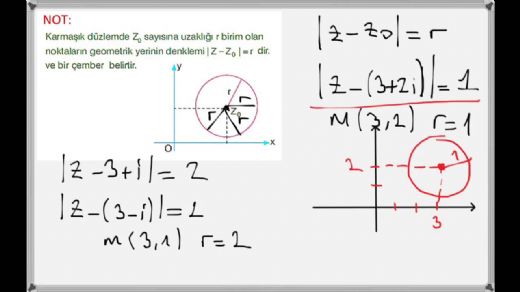
Karmaşık bir sayının modülü, sayının karmaşık düzlemdeki uzaklığını ifade eder. "z = a + bi" karmaşık sayısının modülü şu şekilde hesaplanır:

• |z| = √(a² + b²)

Ayrıca, karmaşık sayının konjugatı, sanal kısmın işaretinin değiştirilmesiyle elde edilir. "z = a + bi" için konjugat "z̅ = a - bi" şeklindedir.

Karmaşık sayılar, birçok alanda önemli uygulamalara sahiptir:

• Elektrik mühendisliğinde, alternatif akım analizi için kullanılır.
• Kontrol sistemlerinde, sistemin kararlılığını belirlemede yer alır.
• Fiziksel sistemlerde dalga hareketleri ve kuantum mekaniği gibi konularda kullanılır.

Karmaşık sayılar, matematiğin ve mühendisliğin birçok alanında önemli bir rol oynamaktadır. Bu sayılar, reel sayıların sınırlamalarını aşarak daha karmaşık ve çeşitli problemleri çözme imkânı sunar. Karmaşık sayılar, temel matematiksel işlemlerle birlikte, mühendislik ve fizik gibi uygulama alanlarında geniş bir yelpazeye sahiptir. Bu nedenle, karmaşık sayıların anlaşılması, matematiksel düşünceyi geliştirmek ve problem çözme becerilerini artırmak için kritik öneme sahiptir.