
Köklü Sayılar Konu Anlatımı
Köklü sayılar, matematiğin temel kavramlarından biridir ve özellikle cebirsel işlemlerde önemli bir rol oynamaktadır. Bu makalede, köklü sayıların tanımı, özellikleri, işlemleri ve çeşitli uygulamaları detaylı bir şekilde incelenecektir. Matematiksel düşünme becerilerini geliştirmek için köklü sayıları anlamak kritik öneme sahiptir.
Köklü Sayılar Konu Anlatımı Köklü sayılar, matematiğin temel unsurlarından biri olup, özellikle cebirsel ifadelerde sıklıkla karşımıza çıkan bir kavramdır. Bu makalede köklü sayıların tanımı, özellikleri, işlemleri ve uygulamaları detaylı bir şekilde ele alınacaktır. Köklü Sayıların Tanımı Köklü sayılar, bir sayının karekökü, küp kökü veya daha yüksek dereceli kökleri olarak tanımlanabilir. Genel bir ifade ile, n. dereceden kök, a sayısının n. dereceden kökü, a sayısının n. kuvvetine eşit olan bir sayıdır. Matematiksel olarak, bu ifade şu şekilde yazılabilir:
Köklü sayılar, genellikle pozitif reel sayılar arasında tanımlanır; ancak negatif sayılar için kök alma işlemi, yalnızca çift dereceli köklerde reel sayılar için uygulanamaz. Köklü Sayıların Özellikleri Köklü sayıların bazı temel özellikleri şunlardır:
Bu özellikler, köklü sayıların farklı matematiksel işlemler içinde kullanılmasını kolaylaştırır. Köklü Sayılarla İşlemler Köklü sayılarla yapılan işlemler, diğer sayı türlerinde olduğu gibi toplama, çıkarma, çarpma ve bölme işlemlerini içerir. Ancak, köklü sayılarla yapılan bu işlemler, belirli kurallara ve özelliklere bağlıdır.
Köklü Sayıların Uygulamaları Köklü sayılar, birçok alanda önemli uygulamalara sahiptir. Bu uygulamalar, matematiksel hesaplamalardan mühendislik, fizik ve istatistik gibi alanlara kadar geniş bir yelpazeyi kapsamaktadır. Örneğin:
Sonuç Köklü sayılar, matematiksel işlemler ve uygulamalar açısından son derece önemli bir kavramdır. Tanımları, özellikleri ve işlemleri konusunda derinlemesine bir anlayışa sahip olmak, öğrencilerin ve araştırmacıların matematiksel düşünme becerilerini geliştirmelerine katkıda bulunacaktır. Köklü sayıların daha iyi anlaşılması, karmaşık matematiksel problemleri çözmede kritik bir rol oynamaktadır. Bu nedenle, köklü sayılar üzerine yapılan çalışmalar ve araştırmalar, matematik alanında önemli bir yer tutmaktadır. |
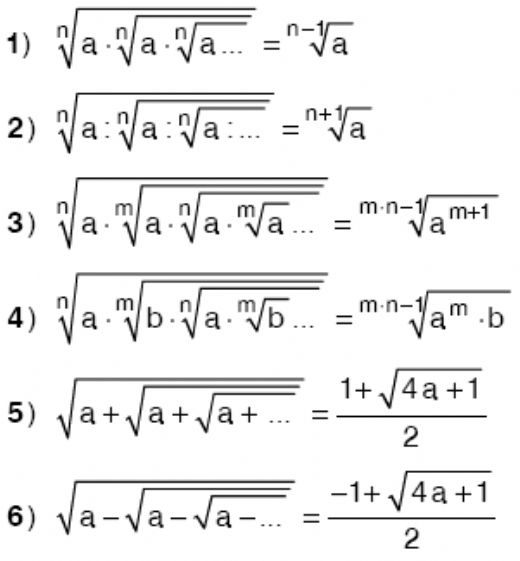
































Köklü sayılar konusunu öğrendiğimde, bu ifadelerin matematikteki önemini daha iyi anladım. Özellikle köklü sayıların tanımının ve özelliklerinin net bir şekilde açıklanması çok faydalı oldu. Örneğin, n sayısının tek olması durumunda a sayısının n. dereceden kökünün daima reel bir sayı olması gerçeği, işlemler yaparken dikkat etmem gereken bir nokta. Ayrıca toplama ve çıkarma işlemlerinin sadece benzer köklü ifadeler arasında yapılabileceği bilgisi de çok önemli. Bu tür ayrıntılar, köklü sayılarla işlem yaparken karşımıza çıkabilecek hataları önlememize yardımcı olabilir. Kısacası, köklü sayılar konusunu öğrenmek, matematiksel becerilerimi geliştirmemde büyük bir rol oynadı. Sizce köklü sayılarla ilgili diğer hangi önemli noktaları öğrenmek faydalı olabilir?
Öğrenim Süreci
Asri, kütlü sayılar konusunu öğrenmen gerçekten çok değerli. Bu tür matematiksel kavramların anlaşılması, ileride daha karmaşık konulara geçişte büyük önem taşıyor. Kök sayılarla ilgili belirttiğin noktalar, temel matematik bilgilerini pekiştirmek açısından oldukça faydalı.
Önemli Noktalar
Kök sayılarla ilgili öğrenilmesi gereken diğer önemli noktalar arasında, kütlü sayıların çarpma ve bölme işlemlerinin nasıl gerçekleştirileceği, köklü ifadelerin sadeleştirilmesi ve farklı derecelerdeki köklerin birbirleriyle ilişkileri bulunuyor. Ayrıca, köklerin üslü ifadelerle bağlantısını anlamak da, işlemlerin daha kolay yapılmasını sağlar.
Uygulama ve Pratik
Bu bilgilerin yanı sıra, pratik yaparak kütlü sayılarla ilgili problemleri çözmek de öğrenimini pekiştirecektir. Farklı türden sorular üzerinde çalışmak, hem teorik bilgilere hakim olmanı sağlar hem de bu bilgileri gerçek hayat problemlerine uygulama yeteneğini geliştirir.
Sonuç olarak, kütlü sayılar konusundaki bilgi birikimini artırmak için bu noktaları da göz önünde bulundurabilirsin. Başarılarının devamını dilerim!