
6 Sınıf Matematik Konu Anlatımı ve İçeriği
6. sınıf matematik, öğrencilerin temel matematik bilgilerini pekiştirdiği ve yeni kavramlarla tanıştığı kritik bir dönemdir. Bu süreçte sayılar, cebirsel ifadeler, geometri, veri analizi ve olasılık gibi konular detaylı bir şekilde işlenir. Öğrenciler, problem çözme becerilerini geliştirirken matematiksel düşünme yeteneklerini de güçlendirirler.
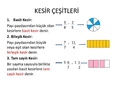
6 Sınıf Matematik Konu Anlatımı ve İçeriği 6. sınıf matematik, öğrencilerin temel matematik bilgilerini pekiştirmeleri ve yeni kavramlarla tanışmaları için kritik bir dönemdir. Bu aşamada, öğrenciler matematiksel düşünme becerilerini geliştirmeye ve çeşitli matematiksel kavramları anlamaya yönelik önemli adımlar atarlar. Bu makalede, 6. sınıf matematik müfredatında yer alan başlıca konular detaylı bir şekilde ele alınacaktır. 1. Sayılar ve İşlemler Bu bölüm, doğal sayılar, tam sayılar, kesirler ve ondalık sayılar gibi farklı sayı türlerine odaklanır. Öğrenciler, sayıların özelliklerini öğrenir ve çeşitli matematiksel işlemleri (toplama, çıkarma, çarpma, bölme) gerçekleştirme yeteneklerini geliştirirler.
2. Cebirsel İfadeler Cebirsel ifadeler, sayılar ve harflerin bir arada kullanıldığı matematiksel ifadelerdir. Öğrenciler, değişkenler ile işlem yapmayı öğrenir ve cebirsel ifadeleri sadeleştirme, toplama ve çıkarma gibi işlemleri gerçekleştirme becerisi kazanırlar.
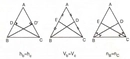
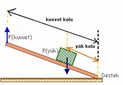
3. Geometri Geometri, şekillerin, alanların ve hacimlerin incelendiği bir matematik dalıdır. 6. sınıf öğrencileri, temel geometrik kavramları öğrenir ve iki boyutlu ile üç boyutlu şekillerin özelliklerini keşfederler.
4. Veri Analizi ve Olasılık Veri analizi, elde edilen verilerin düzenlenmesi ve yorumlanması ile ilgilidir. Olasılık ise rastgele olayların olma ihtimalini inceler. Bu bölüm, öğrencilerin veri toplama, düzenleme, grafiklerle gösterme ve olasılık hesaplama konularında bilgi edinmelerini sağlar.
5. Problemler ve Uygulamalar Matematiksel problemleri çözme, öğrencilerin analitik düşünme yeteneklerini geliştirmelerine yardımcı olur. Bu bölümde, sözel problemler, sayısal problemler ve matematiksel modelleme konularına yer verilir.
Sonuç 6. sınıf matematik dersi, öğrencilerin matematiksel düşünme becerilerini geliştirmeleri ve temel matematik kavramlarını anlamaları açısından son derece önemlidir. Bu dönemde edinilen bilgi ve beceriler, ilerleyen yıllarda daha karmaşık matematik konularını öğrenmelerine zemin hazırlar. Öğrencilerin aktif katılımı sağlanmalı, problem çözme becerileri geliştirilmelidir. Eğitimcilerin, öğrencilerin ilgi ve ihtiyaçlarına göre ders içeriklerini çeşitlendirmeleri, öğretim sürecini daha etkili hale getirecektir. |











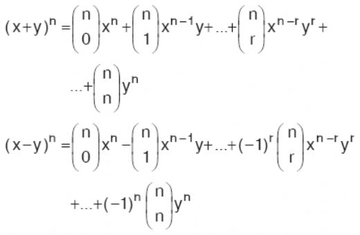





















Matematik problemlerini anlamakta zorluk yaşıyorum ve özellikle çözüm stratejilerini nasıl geliştirebilirim? Özellikle zor soruları çözmek için hangi adımları takip etmek gerekir?
Amir, matematik problemlerini anlamakta zorlanmak oldukça yaygın bir durumdur ve çözüm stratejilerini geliştirmek için bazı adımlar izlemek faydalı olabilir. İlk olarak, problemin neyi sorduğunu tam olarak anlamak önemlidir. Problemi dikkatlice oku ve anahtar kelimeleri belirle.
Daha sonra, problemin hangi matematiksel kavramlara dayandığını belirle. Örneğin, geometri, cebir ya da olasılık teorisi gibi konuların hangisiyle ilgili olduğunu anlamaya çalış. Bu kavramlarla ilgili temel bilgilerini gözden geçirmek faydalı olabilir.
Bir sonraki adım, problemi daha küçük ve yönetilebilir parçalara bölmektir. Büyük bir problemi küçük adımlara bölerek çözmek, her bir adımı daha kolay hale getirebilir.
Doğru stratejiyi belirlemek için benzer örnekleri inceleyebilir ve çözüm yollarını inceleyebilirsin. Ayrıca, problem üzerinde çalışırken farklı yöntemler denemekten kaçınmamalısın. Bazen farklı bir bakış açısı, çözümü daha kolay hale getirebilir.
Son olarak, çözümünü kontrol etmeyi unutma. Yapabileceğin hataları düzeltmek için çözümünün üzerinden geçmek, öğrenme sürecinin bir parçasıdır.
Umarım bu adımlar problemleri çözmede sana yardımcı olur. Başarılar dilerim!