Geometri Konu Anlatımı
Geometri, uzay veya uzayda bulunan cisimlerin, şekillerin yeryüzünde kapladıkları alanların ve yüzeylerin hesaplanmasını inceleyen bir matematik bilim dalının alt dalı olarak bilinir. Kelime olarak "geometri" herhangi bir alanın ölçülmesi anlamına gelmektedir. Geometri dersi, lise grubunda bulunan öğrencilere anlatımı yapılan bir ders olmaktadır. Öğrencilerin en fazla zorlandığı dersler arasında yer almaktadır. Geometri dersi, öğrenciler için oldukça çözülmesi zor olan sorular içermektedir. Geometri soru tarzları, tek çözüm yolu ile çözülmesi gerektiği gibi birçok kuralı da kullanarak çözülebilir. Her soru, kendine uygun olan metot ve formül uygulanması ile çözülmelidir. Geometri dersine ait çok sayıda formül bulunduğu için ezber yapılması yerine öğrencinin bu formülleri soru üzerinde pratik yaparak öğrenmesi daha faydalı olacaktır. Ayrıca, geometri sorularında öğrencinin soruya dair ne tür bir çözüm uygulaması gerektiğini kendi iradesi ile görmesi gerekmektedir. Eğer öğrenci kendi çözüm noktasını göremezse, o soru öğrenci için başlı başına bir eziyet ve zor olan bir ders olmaktan başka bir şey olmamaktadır.
Geometri Konu Anlatımı ve İçeriği
1. Ünite: Geometrik Kavramlar
Bu ünitede geometrinin temelini oluşturan kavramlar anlatılmaktadır:- Nokta
- Doğru
- Düzlem
- Işın
- Doğru Parçası
- Yarı Doğru
- Açılar
- Açı Ölçü Birimleri
- Açıortay
- Tümler Açı
- Bütünler Açı
- Ters Açılar
- Paralel Doğrular
2. Ünite: Özel Üçgenler
Bu ünitede dik üçgen, pisagor bağıntısı, ikizkenar üçgen, öklit bağıntıları ve eşkenar üçgen konularının anlatımı yapılmaktadır.
3. Ünite: Açıortay
Üçgende açıortay bağıntıları başlığı altında:- İç Açıortay Bağıntısı
- İç Açıortay Uzunluğu
- Dış Açıortay Bağıntısı
- Dış Açıortay Uzunluğu
- İç Açıortay ile Dış Açıortay Arasındaki Açı
konuları anlatılmaktadır.
4. Ünite: Üçgende Benzerlik
Üçgende benzerlik ünitesinde:- Eş Üçgenler
- Açı-Açı Benzerlik Teoremi
- Kenar-Açı-Kenar Benzerlik Teoremi
- Kenar-Kenar-Kenar Benzerlik Teoremi
- Temel Benzerlik Teoremi
- Tales Teoremi
- Benzerlik Oranları
Ayrıca özel teoremler başlığı altında ise Menelaus ve Seva teoremlerinden bahsedilmektedir.
5. Ünite: Çokgenler
Bu ünitede:- İçbükey Çokgenler
- Dışbükey Çokgenler
- Düzgün Çokgenler
- Paralel Kenar
- Dikdörtgen
- Deltoid
- Üçgenler
- Dörtgenler
- Eşkenar
- Kare
- Yamuk
gibi cisimlerin uzunluk ve alan hesaplanması anlatılmaktadır.
6. Ünite: Çemberde Açı
Bu ünitede:- Çember ile Daire Arasındaki Fark
- Çemberde Açı Özellikleri
- Merkez Açı
- Çevre Açı
- Teğet-Kiriş Açı
- İç Açı
- Dış Açı
- Kirişler Dörtgeni
konuları ele alınmaktadır.
7. Ünite: Katı Cisimler
Bu ünitede:- Silindir
- Piramitler
- Koniler
- Küreler
- Prizmalar
gibi şekillerin yüzey alanları ve toplam alanları hesaplanması anlatılmaktadır.
8. Ünite: Doğrunun Analitiği
Bu başlık altında:- İki Noktası Bilinen Doğrunun Eğimi ve Denklemi
- Bir Noktası ve Eğimi Bilinen Doğrunun Denklemi
- Eksenlere Paralel Doğruların Denklemi
- Eksenleri Kestiği Noktaları Bilinen Doğruların Denklemi
- Doğruların Grafikleri
konuları anlatılmaktadır.
9. Ünite: Daire Alanı ve Çevresi
Bu ünitede:- Daire Diliminin Alanı ve Yay Parçasının Uzunluğu
- Daire Kesmenin Alanı
- Daire Halkasının Alanı
konu anlatımı yapılmaktadır.
|
Abdülaziz
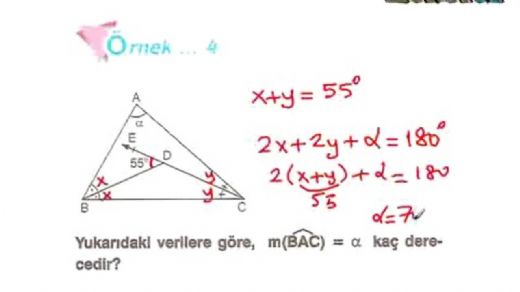
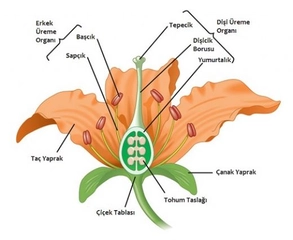
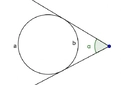
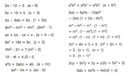
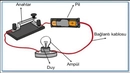
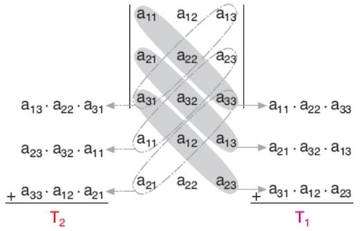
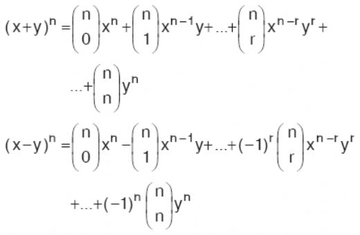
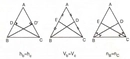
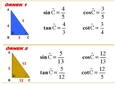
12 Temmuz 2024 CumaGeometri dersinde anlatılan bu konuları anlamakta çok zorlanıyorum. Özellikle benzerlik teoremleri ve üçgen bağıntıları konularında kafam karışıyor, bu konuları daha iyi anlamak için ne yapmalıyım?
Cevap yazAdmin
12 Temmuz 2024 CumaMerhaba Abdülaziz,
Geometri dersinde zorlandığın konuları daha iyi anlamak için öncelikle temel kavramlara hakim olman önemli. Benzerlik teoremleri ve üçgen bağıntılarını daha iyi anlamak için şu adımları takip edebilirsin:
1. Temel Kavramları Tekrar Et: Bu konuların temelinde yer alan kavramları ve tanımları iyice öğren. Örneğin, benzerlik oranı ve üçgenlerin özellikleri gibi.
2. Örnek Çözümler: Çeşitli kaynaklardan örnek sorular çözerek farklı soru türleriyle karşılaş. Bu, konuyu nasıl uygulayacağını gösterecektir.
3. Görsel Çalışmalar: Konuların görsel materyallerle desteklenmiş anlatımlarını izlemek, kavramları daha iyi anlamana yardımcı olabilir.
4. Grupla Çalışma: Arkadaşlarınla bir araya gelerek birlikte çalışmak, birbirinize sorular sorarak konuları daha iyi anlamanıza yardımcı olabilir.
5. Öğretmenine Danış: Anlamadığın yerleri öğretmenine sorarak açıklama istemekten çekinme.
Bu adımları takip ederek daha iyi bir kavrayışa ulaşabileceğine inanıyorum. Başarılar dilerim!