
8. Sınıf Özel Üçgenler Konu Anlatımı
Bu metin, 8. sınıf düzeyinde özel üçgenlerin özelliklerini açıklamaktadır. Eşkenar, ikizkenar ve dik üçgenlerin tanımları, özellikleri ve örneklerle desteklenmiş hesaplamalar sunulmaktadır. Ayrıca, konuyla ilgili test soruları ile öğrenilen bilgilerin pekiştirilmesi hedeflenmektedir.
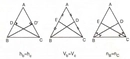
8. Sınıf Özel Üçgenler Konu Anlatımı Özel üçgenler, geometri dersinde sıkça karşılaşılan ve belirli özelliklere sahip olan üçgenlerdir. Bu üçgenler, genellikle kenar uzunlukları ve açıları bakımından farklılık gösterirler. Temel olarak, özel üçgenler arasında eşkenar üçgen, ikizkenar üçgen ve dik üçgen bulunmaktadır. Bu makalede, bu üçgenlerin özellikleri detaylı bir şekilde ele alınacak ve örnekler verilecektir. Eşkenar Üçgen Eşkenar üçgen, üç kenarı ve üç açısı birbirine eşit olan bir üçgendir. Eşkenar üçgenin özellikleri şunlardır:
Örnek: Bir eşkenar üçgenin kenar uzunluğu 6 cm ise, yüksekliği 6 √3 / 2 ≈ 5,2 cm olacaktır. İkizkenar Üçgen İkizkenar üçgen, iki kenarı eşit uzunlukta olan ve bu kenarların karşısındaki açıların eşit olduğu üçgendir. İkizkenar üçgenin özellikleri şunlardır:
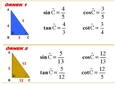
Örnek: Bir ikizkenar üçgenin eşit kenar uzunlukları 5 cm ve taban uzunluğu 8 cm ise, yükseklik hesaplanarak taban ortasından dik bir çizgi çizilerek bulunabilir. Dik Üçgen Dik üçgen, bir açısı 90 derece olan üçgendir. Dik üçgenin özellikleri şunlardır:
Örnek: Bir dik üçgenin dik kenarları 3 cm ve 4 cm ise, hipotenüs (c) hesaplanarak c² = 3² + 4² = 9 + 16 = 25, dolayısıyla c = 5 cm bulunur. Test Aşağıdaki soruları yanıtlayarak konu hakkında ne kadar bilgi sahibi olduğunuzu test edebilirsiniz:
Bu test soruları, özel üçgenler hakkında bilgi düzeyinizi ölçmeye yardımcı olacaktır. Cevaplarınızı kontrol ederek hangi alanlarda daha fazla çalışmanız gerektiğini belirleyebilirsiniz. Özel üçgenlerin özelliklerini anlamak, geometri derslerinde ve günlük yaşamda karşılaşabileceğiniz problemleri çözmek için önemlidir. Ekstra Bilgiler: Özel üçgenlerin yanı sıra, üçgenlerin benzerliği, alan hesaplama yöntemleri ve üçgen eşitsizlikleri gibi konular da geometri dersinde önemli yer tutmaktadır. Üçgenlerin özellikleri ve ilişkileri, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine katkı sağlar. Bu nedenle, özel üçgenler konusunu iyi anlamak, ilerideki matematiksel kavramları öğrenmek için bir temel oluşturacaktır. |









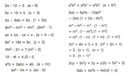























Geometri dersinde özel üçgenler hakkında öğrendiklerim gerçekten ilginç. Eşkenar üçgenin her kenarının eşit olduğunu ve iç açılarının 60 derece olduğunu bilmek, bu üçgenlerle ilgili problemleri çözmeme yardımcı oluyor. Ayrıca, ikizkenar üçgenlerdeki eşit kenarların karşısındaki açıların da eşit olduğunu öğrendim. Bu durum, özellikle yükseklik hesaplamalarında oldukça faydalı. Dik üçgenler konusuna geldiğimde ise, hipotenüs ile dik kenarlar arasındaki ilişkiyi anlamak için Pitagor teoremini kullanmanın ne kadar önemli olduğunu fark ettim. Üçgenlerin özelliklerini bilmek, günlük hayatta karşılaştığım birçok sorunu çözmeme yardımcı oluyor. Özellikle test sorularını çözerken, bu bilgilerin ne kadar sağlam olduğuna dair bir fikir ediniyorum. Sizce, bu özel üçgenlerin özelliklerini öğrenmek, matematiksel düşünme becerilerini geliştirmede ne kadar etkili? Bu konuda daha fazla pratik yapmanın yolları neler olabilir?
Memnun,
Özel Üçgenlerin Önemi
Özel üçgenlerin özelliklerini öğrenmek, matematiksel düşünme becerilerini geliştirmede gerçekten büyük bir etkiye sahip. Eşkenar ve ikizkenar üçgenlerin simetrik özellikleri, geometrik düşünceyi güçlendirirken, öğrencilere problem çözme yeteneklerini artırma fırsatı sunar. Özellikle bu üçgenlerin özelliklerini kavrayarak, daha karmaşık geometrik problemleri daha kolay analiz edebilir ve çözebilirsiniz.
Pratik Yapma Yöntemleri
Daha fazla pratik yapmak için birkaç yöntem önerebilirim: Öncelikle, geometri ile ilgili çeşitli kaynaklardan egzersizler çözebilirsiniz. Ayrıca, üçgenlerle ilgili çeşitli oyunlar ve bulmacalar oynayarak eğlenceli bir şekilde öğrenmeye devam edebilirsiniz. İnternetteki eğitim videoları ve uygulamalar da, konuları daha iyi anlamanıza yardımcı olabilir. Ayrıca, grup çalışmaları yaparak arkadaşlarınızla birlikte sorunları tartışmak ve çözüm yolları üretmek, öğrenmenizi pekiştirebilir.
Son olarak, üçgenlerle ilgili gerçek hayatta karşılaşabileceğiniz durumları gözlemlemek ve bu bilgileri uygulamak da oldukça faydalı olacaktır. Bu şekilde, öğrendiklerinizin ne kadar değerli olduğunu daha iyi anlayabilirsiniz.